Understanding the Mohr-Coulomb Criterion in Geology

In the world of geology and engineering geology, understanding the fundamental principles and criteria that govern soil and rock behavior is crucial. One such criterion that plays a pivotal role in geotechnical engineering is the Mohr-Coulomb criterion. In this comprehensive guide, we will delve deep into the concept, its significance, and practical applications.
Introduction
Geotechnical engineering is a field that deals with the study of soil and rock mechanics. It plays a crucial role in construction, foundation design, and slope stability assessments. Among the various principles and criteria used in geotechnical engineering, the Mohr-Coulomb criterion is a cornerstone concept. It provides essential insights into the behavior of soils and rocks under different conditions.
What is the Mohr-Coulomb Criterion?
The Mohr-Coulomb criterion, named after its developers, the German engineer Otto Mohr and the French engineer Charles-Augustin de Coulomb, is a fundamental concept used to analyze and predict the failure of materials, particularly soil and rock. It is a graphical representation of the relationship between normal stress (σ) and shear stress (τ) on a material plane. This relationship is crucial in determining the conditions under which materials will fail.
The Mohr-Coulomb criterion is often expressed as:
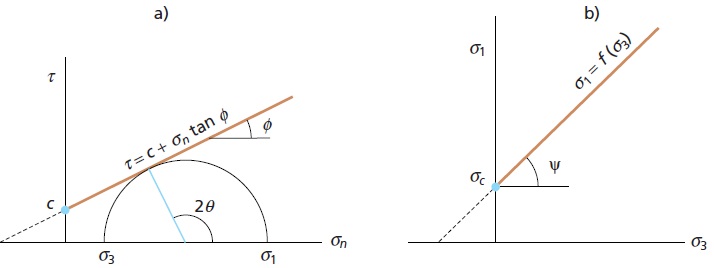
τ = c + σn tan φ
where:
τ and σn are the normal and shear stresses on the failure plane
c and φ are the cohesion and internal friction angle of the intact rock
The criterion can also be expressed as a function of the principal stresses σ1 and σ3 (Figure 1):
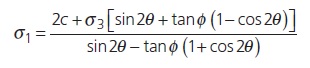
from which the strength on any plane defined by θ can be obtained. For the critical failure plane θ = 45°+φ/2, the equation above will now be:
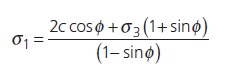
If σ3 = 0, σ1 will be the uniaxial compressive strength of the rock:
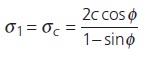
By extension (Figure 1b) the criterion also gives the tensile strength value:
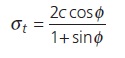
Key Components of the Mohr-Coulomb Criterion
To gain a deeper understanding of this criterion, let’s break down its key components:
Cohesion (c)
Cohesion represents the inherent strength of the material. It is the shear stress at which the material will fail when no normal stress is acting on it. Materials with high cohesion require a significant shear stress to fail, while those with low cohesion are more susceptible to failure.
Angle of Internal Friction (φ)
The angle of internal friction is a measure of how a material’s resistance to shear stress changes with the application of normal stress. Materials with a higher angle of internal friction can withstand higher shear stresses under the influence of normal stress.
Understanding Shear Strength
Shear strength is a critical parameter in geotechnical engineering, and the Mohr-Coulomb criterion is a valuable tool for assessing it. Shear strength represents the maximum shear stress a material can withstand without undergoing failure. It varies with factors such as material composition, stress conditions, and pore water pressure.
Practical Applications
The Mohr-Coulomb criterion finds extensive applications in geotechnical engineering and related fields:
1. Foundation Design
In foundation engineering, understanding the shear strength of the underlying soil is essential for designing stable foundations. Engineers use the Mohr-Coulomb criterion to assess soil stability and design foundations that can support the intended structures.
2. Slope Stability Analysis
For projects involving slopes, such as embankments or natural slopes, slope stability analysis is critical. The Mohr-Coulomb criterion helps engineers determine whether a slope is stable or likely to experience failure due to factors like rainfall or seismic activity.
3. Retaining Wall Design
Designing retaining walls that can withstand the lateral pressure of soil requires a thorough understanding of shear strength. Engineers use the criterion to calculate the required wall strength and optimize designs.
Factors Affecting the Mohr-Coulomb Criterion
Several factors influence the Mohr-Coulomb criterion’s applicability and results:
1. Material Properties
The cohesion and angle of internal friction are material-specific properties. Different types of soils and rocks exhibit varying Mohr-Coulomb behavior.
2. Stress Conditions
The normal and shear stresses acting on a material plane play a crucial role in determining its behavior. Changes in stress conditions can lead to different outcomes.
3. Pore Water Pressure
The presence of water within soil can affect its shear strength. Elevated pore water pressure can reduce the effective stress and, consequently, shear strength.
Conclusion
The Mohr-Coulomb criterion is a fundamental concept in geology and engineering geology, offering valuable insights into the behavior of soils and rocks under different conditions. Engineers and geologists rely on this criterion for designing stable foundations, assessing slope stability, and optimizing retaining wall designs, among other applications.
In the world of geotechnical engineering, a solid grasp of the Mohr-Coulomb criterion is essential for ensuring the safety and stability of various structures and projects.
Sources
- Terzaghi, K., & Peck, R. B. (1967). Soil Mechanics in Engineering Practice. John Wiley & Sons.
- Das, B. M. (2008). Principles of Geotechnical Engineering. Cengage Learning.
- Craig, R. F. (2013). Soil Mechanics. John Wiley & Sons.
This article has been compiled using information from reputable sources in the field of geotechnical engineering.
Read more on blog: